Hasenspiel - Escape the White Rabbit

Hasenspiel (German for “Rabbit Game”) is relatively simple game played on the chess board with 5 pawns. The goal is for the white pawn a.k.a. the rabbit to escape the opponent pawns. It’s a funny and not so trivial game. In this article, we will see how to completely solve it with an efficient implementation in C.

Game Rules

Initial Position
Initial Position in Hasenspiel
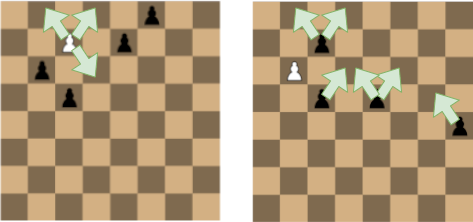
Possible moves
Possible moves for white (left) and black (right) in given positions
Examples of victories
Left: white wins, it could escape to the opposite raw. Right: black wins, it could completely encircle white

Pretty easy so far. You can play it online here.

Considerations on the Hasenspiel

The origin of this game is quite obscure. It was introduced to me by an acquaintance from Eastern Germany, thus it comes probably from there. I couldn’t find any resembling game searching on Google. If you are aware of one, please tell me.

This game is a good example of a Markov Decision Process (MDP) with two players and perfect information: all a player needs to know to decide a move lays open on the board. It has the Markov property, means the current state (board configuration + player on turn) is the only information required to estimate what could follow, no matter how this state was reached. Only the present state is relevant to make decisions, not the paste states. This has its importance in solving this game, as we will see later.

Other fact worth noticing: At the end of the game, there is one winner, and only one. No draw or whatever. This is also important in assessing if a player can force victory from a given position.

Last but not least: there is no exogenous randomness (e.g. dice roll) contributing to the game. Any state is the result of the decisions of the players only.

Questions

After playing a certain number of games, it seems however intuitive that black can force victory if it makes no mistake, but that it can easily make a mistake leading white to escape and win. Can we prove it?

The second question that arises is, can we define an optimal policy, means an optimal way to play at any given state for both black and white?

The third question is, how many possible states, means board configurations, are possible in this game? How many possible games are there?

Methodology

To answer those questions, we need to simulate all possible hasenspiel games. However, the number of possible games is too massive for a direct “bruteforce” approach. Thus the strategy is to follow a depth-first search (DFS) approach. White plays its first possible move, then black its first possible move, etc. until the game reaches a final step where one of both players wins, from there we go up one step, explore the second last possible move, etc, until we have explored all possible nodes of the game. For each state, we store following information:

Nodes update

Nodes represent states. The children of a node are the states that can be reached from this state through the possible actions (moves) of the player at turn at this state. The nodes are updates recursively following the depth-first search, starting from the final nodes, where a player wins, backward to its parent node.

A final node has a number \(N=1\) of possible games, with a proportion \(p=1\) of winning games for the player that won at this node, and \(F=true\) for this winning player, means the player who wins there can force the victory there (obviously).

Then for a parent node:

Node update
Black position leading here to two white position: the number of possible games is the sum of the number of possible game of its child nodes; same for the number of games where black wins. Here one of the possible black actions leads to a white position where black can force victory, thus black can force.

If a node has already been evaluated during the search and is reached through another path: no need to go down this node again, you can re-use its already computed values. This is due to the Markov property mentioned above, and saves a massive amount of computation.

This way you go down to all the final nodes, up to the top node representing the start position, through all the intermediate nodes.

[UPDATE] Actually just knowing which player can force victory in which position is a bit limited. We would like to quantify this. For this, we compute a state value for each position, differentiated by player. For example, such state as such value for black and such value for white. This state value should also be 0 for a player if it can’t force victory from there. The idea is a bit the same than previously, augmented with idea from dynamic programming / reinforcement learning. In reinforcement learning, you can define a discount factor \(\gamma\) correcting the reward depending on in how many steps the reward is reached. If the reward \(R\) is reached in \(n\) steps, from the current state, it will contribute by \(\gamma^{-n}.R\) to the value of this state (\(\gamma \in (0, 1]\)). Thus, we define a reward of 1 when a player reached a state where he won. When backward-propagating those rewards to states further up who led to victory (or defeat), we don’t directly apply a reward factor \(\gamma^{-n}\), but instead we take \(V := n + 1\). If \(V > 0\), it is thus incremented by one each time it’s back-forwarded to its parent state. The parent state gets all the values \(V\) of its children states and performs following operation: it takes the MIN of the state values of the opposite player, and the MAX of its own state values. For example, if it’s a state where black is at turn, it will take the MAX of the black state values of its children states, and the MIN of the white state values of its children states. The subtlety here is how to define MIN and MAX. \(n\) here represents the negative of the exponent of the discount factor, and 0 represents a defeat, so we end up with following ordering of the positive integers:

And the previous MIN and MAX are defined according to this order.

The good thing is, \(V_b(s) > 0\) i.i.f. \(V_w(s) = 0\) (and reversely, where \(V_b(.)\) is the state value for black and \(V_w(.)\) the state value for white). Thus for each state we just need to encode one value, an integer where the first bit encodes for which player this value is, and the following bits encoding the value itself (then implicitly the value of the opposite player for this state is 0).

This state value can be interpreted this way: \(V_b(s) > 0\) meansblack can force victory from state \(s\) in max. \(V_b(s)\) moves. And the policy for each player is straight forward: if there are following states with a positive value, go to the state with the smallest value (which is the biggest according to our ordering). If not, go to the state with the worse positive value for the opponent.

Thus the value of a move in a given position is evaluated based on its afterstate.

What we call here optimal policy, is when an agent (player) performs the resulting highest ranking action.

In a previous version, the player who could not force victory chosed the move where it had the highest percentage of winning games starting from the resulting position. It was basically an exhaustive Monte-Carlo Tree search value wise without discounting. The problem was, the opponent could sometimes directly win in one move from the resulting position, which made the program look quite dumb: it was looking at the move which optimized for absolutely all games starting from there, no matter if one of them was directly obviously losing. Optimizing with the method presented here avoids this pitfall: if one move leads to a position where the opponent can win directly, means the resulting position has vakue 1 for the opponent (the highest possible value in our ordering) and another move is not directly winning for the opponent, it will chose the other move. Thus the program feels also stronger. Even when playing white, it often puts black in position where it has e.g. 6 possible moves, but only one of them where black can keep on being able to force victory.

Only one good move for black
Screenshot from my app. Here black has 6 possible moves, but only one of them where black can continue forcing victory, all the other moves make white able to force victory. Can you find this move?

Answers

The interesting fact is, although black can force its way to victory from the beginning, this way is very narrow, and a single mistake makes his situation pretty hopeless. That makes this Hasenspiel pretty interesting.

And this was computed in… 0.143 seconds, on a single Intel(R) Core(TM) i5-10300H CPU @ 2.50GHz. Blazingly fast. See the next section.

Implementation

This program is implemented in C (code available here) and makes quite intensive use of bitwise operations and macro-functions. A quite common opinion is that macros are evil, or even programming masochism, but personally I like them. More on it on a next blog post maybe.

State representation

In every state of the game, all the pawns can only be on black squares, since they start on black square and can move only diagonally (easy inductive reasoning). There are 32 black squares on a standard chess board, numbered from 0 to 31, from left to right upward. Thus the position of a single pawn can be encoded in five bits (\(2^5=32\)), and the position of the five pawns on the board in 25 bits. Then, one more bit is required to encode the player at turn at this position. Thus 26 bits in total. This fits in a 32 bits unsigned integer type, a.k.a. uint32_t.

The position encoding is ordered as follows:

The descending order for encoding the position of the black pawns has two major advantages:

  1. Position disambiguation: pawn 1 at position 4 and pawn 2 at position 8 for example is exactly the same as pawn 1 at position 8 with pawn 2 at 4. Thus by enforcing order, you prevent that various encodings encode the same position
  2. The numerical value of the variable encoding the state is minimized, having the lowest value on the highest bits.

If white is at turn, it has max. 4 possible moves available (one move diagonally in every direction). Black has max. 8 possible moves. Thus all possible moves in any given state can be one-hot encoded in a single uint8_t variable.

Their are several pitfalls to be aware of, such as moves restricted for pawns on an edge, or move translation depending on the parity of the raw, e.g. move forward right means adding +4 to the position on even rows and +5 on odd rows. Also, when white wins, the game is not computed until it reaches the first row, but only until it passes by the last black pawn, where it is obvious that white is unstoppable from there. And many other tricks, leading to the performance mentioned above.

In order to store the immediate state, it suffices to note that the highest possible numerical value for a position encoding is \(60,614,406\). After subtracting the lowest possible numerical value of a position encoding, you get the size of the array where the nodes are stored during the depth-first search. As mentioned above, there are roughly 776k possible states, means nodes,so that this array stays quite sparse and there are probably ways to map the states in a narrower range of values.

Conclusion

The Hasenspiel is a small game with interesting properties. It is way less complex than chess or go, but also way for complex than tic-tac-toe. Now that it’s completely solved, it allows to test various reinforcement learning approaches like Monte-Carlo, TD learning etc. in a setting where the ground-truth is known.

Its implementation shows also how to make aggressive use of macros and bitwise operations in a defensive programming style, for maximal performance and safety. The game is also easy to extend, for example changing the size of the board, or the number of black pawn. For this it’s enough to change the corresponding macro variables, and possible also switching from uint32_t to uint64_t for representing the states.

Bonus: First 10 moves when bots agents play optimally

After a bit of experience in this game, it seems intuitively that the best strategy for black is to “keep the line”, means maintaining the black pawns on the same horizontal line as much as possible and moving this line forward. This way, the white rabbit has a hard time trying to escape. In the meanwhile, white moves to the middle and then tries to find a hole after coming in contact with black.

But surprizingly, when both players play optimally, white moves forward to the side, and black tries to catch him with only two pawns. See a picture of the first 10 moves when both players play optimally:

First 10 optimal moves
First 10 moves when white and black play optimally

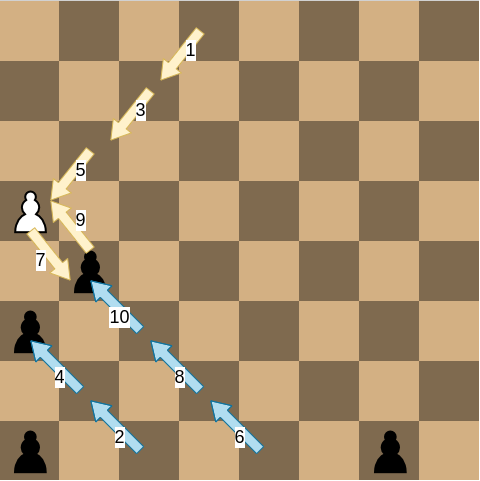
This is another example where the optimal strategy doesn’t match with the human intuition.